Parametric approach to visualize parabolic trajectories

06/04/2023 #tech #science

Join me with a Python-based project that helps visualize parabolic trajectories with user-defined impact points and maximum heights. We’ll talk about the underlying math, parametric equations, and visualization techniques to enhance your understanding of parabolic motion.

Visualizing a Parabola with a Given Impact Point

In this blog post, we will explore a project that calculates the parametric equation of a parabola and visualizes it in three-dimensional space, given a user-defined impact point and maximum height. We will begin with a brief introduction to the mathematics behind the problem and then delve into the details of the project.

Running program angle #1

Mathematical Background

The problem we are trying to solve involves finding a parabolic trajectory that passes through an origin (0,0,0)(0, 0, 0), reaches a given maximum height hmaxh_{max}, and lands at a user-defined impact point (xf,yf,0)(x_f, y_f, 0). To do this, we will use parametric equations to describe the parabola in three-dimensional space. These equations are as follows: x=at2+bt+cx = at^2 + bt + c y=dt2+et+fy = dt^2 + et + f z=gt2+ht+iz = gt^2 + ht + i

Where tt is the parameter that varies along the trajectory.

We know three points on our parabola: the origin (0,0,0)(0, 0, 0), the maximum point (xf2,yf2,hmax)(\frac{x_f}{2}, \frac{y_f}{2}, h_{max}), and the impact point (xf,yf,0)(x_f, y_f, 0). Using these points, we can set up a system of linear equations for each dimension to solve for the coefficients aa, bb, cc, dd, ee, ff, gg, hh, and ii.

Once we have these coefficients, we can construct the parametric equation of the parabolic trajectory as follows: (x(t),y(t),z(t))(x(t), y(t), z(t))

Which can be rewritten as: (at2+bt+c,dt2+et+f,gt2+ht+i)(at^2 + bt + c, dt^2 + et + f, gt^2 + ht + i)

This equation can be directly inputted into graphing software like GeoGebra (or similar) to visualize the trajectory and manipulate it dynamically:

(at^2 + bt + c, dt^2 + et + f, gt^2 + ht + i)

Project Overview

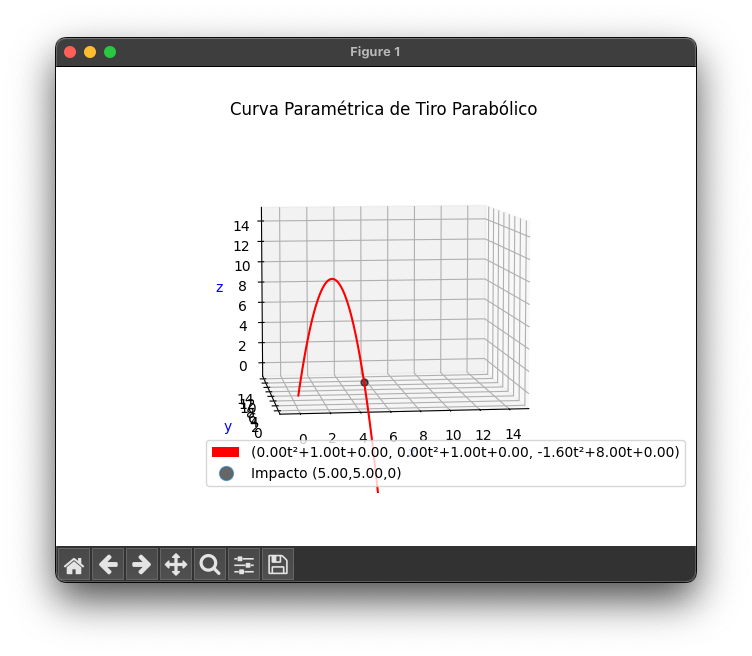
The project takes a user-defined impact point (x,y)(x, y) and the maximum height (hmaxh_{max}), calculates the parametric equation describing the parabola, and then visualizes the resulting graph in three-dimensional space.

Technologies

Dependencies

To install the dependencies:

$ pip install -r requirements.txt

Execution

To run the program:

$ python main.py

Users will need to input the following data:

Source code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
import matplotlib.pyplot as plt
import numpy as np

# Entradas del usuario.
xf = float(input("Coordenada x final: "))
yf = float(input("Coordenada y final: "))
hmax = float(input("Altura máxima: "))

# Planteamiento de matrices del sistema de ecuaciones lineales.
primerMatriz = np.array([
    [0, 0, 1],
    [(xf/2)**2, xf/2, 1],
    [xf**2, xf, 1]
])
segundaMatriz = np.array([
    [0, 0, 1],
    [(xf/2)**2, xf/2, 1],
    [xf**2, xf, 1]
])
tercerMatriz = np.array([
    [0, 0, 1],
    [(xf/2)**2, xf/2, 1],
    [xf**2, xf, 1]
])

# Términos independientes para nuestro sistema de ecuaciones lineales.
terminosIndependientes1 = np.array([0, xf/2, xf])
terminosIndependientes2 = np.array([0, yf/2, yf])
terminosIndependientes3 = np.array([0, hmax, 0])

# Cálculo de las soluciones de los sistemas 3x3
solucionesX = np.linalg.solve(primerMatriz, terminosIndependientes1)
solucionesY = np.linalg.solve(segundaMatriz, terminosIndependientes2)
solucionesZ = np.linalg.solve(tercerMatriz, terminosIndependientes3)

# Imprimir en la terminal la ecuación paramétrica de la parábola resultante.
print("Ecuación paramétrica:")
print(f"({solucionesX[0]:.2f}t²+{solucionesX[1]:.2f}t+{solucionesX[2]:.2f}, {solucionesY[0]:.2f}t²+{solucionesY[1]:.2f}t+{solucionesY[2]:.2f}, {solucionesZ[0]:.2f}t²+{solucionesZ[1]:.2f}t+{solucionesZ[2]:.2f})")

# Creamos la figura de Matplotlib
fig = plt.figure()

# Creamos la gráfica
ax = fig.add_subplot(projection='3d')

# Creamos los ejes.
xx, yy = np.meshgrid(range(20), range(20))

# Creamos el rango de valores para t
t_line = np.linspace(0, 10, 100)

# Planteamos las ecuaciones paramétricas en función de t
x_line = (solucionesX[0] * (t_line ** 2)) + \
    (solucionesX[1] * t_line) + solucionesX[2]
y_line = (solucionesY[0] * (t_line ** 2)) + \
    (solucionesY[1] * t_line) + solucionesY[2]
z_line = (solucionesZ[0] * (t_line ** 2)) + \
    (solucionesZ[1] * t_line) + solucionesZ[2]

# Añadimos el punto de impacto
punto = ax.plot([xf], [yf], [0], markerfacecolor='k',
                markeredgecolor='k', marker='o', markersize=5, alpha=0.6)

# Añadimos las ecuaciones paramétricas a nuestra gráfica en 3D
curva = ax.plot3D(x_line, y_line, z_line,
                  label='Curva Paramétrica', color="red")

# Colocamos los límites de graficación en los ejes.
ax.set_xlim(-1, 15)
ax.set_ylim(-1, 15)
ax.set_zlim(-1, 15)

# Colocamos las etiquetas en los ejes.
ax.set_xlabel('x', color='blue')
ax.set_ylabel('y', color='blue')
ax.set_zlabel('z', color='blue')

# Colocamos el título de la gráfica
ax.set_title("Curva Paramétrica de Tiro Parabólico")

# Proxies para colores de la leyenda.
proxy_grafica = plt.Rectangle((0, 0), 1, 1, fc='r')
proxy_punto = plt.Line2D(
    [0], [0], linestyle="none", marker='o', alpha=0.6, markersize=10, markerfacecolor='black')

# Mostrar la leyenda
ax.legend([proxy_grafica, proxy_punto], [f"({solucionesX[0]:.2f}t²+{solucionesX[1]:.2f}t+{solucionesX[2]:.2f}, {solucionesY[0]:.2f}t²+{solucionesY[1]:.2f}t+{solucionesY[2]:.2f}, {solucionesZ[0]:.2f}t²+{solucionesZ[1]:.2f}t+{solucionesZ[2]:.2f})",
          f"Impacto ({xf:.2f},{yf:.2f},0)"], numpoints=1, loc='lower left')


# Mostramos la gráfica
plt.show()

Credits

This program was created for the Vector Analysis course at the Escuela Superior de Cómputo of the Instituto Politécnico Nacional, taught by Dr. Dárwin Gutiérrez Mejía.

May 2021

Note from 2023.

This project was written in May 2021, however I never had the time to get to write a little about it. If you’re curious about the code and/or the original written report (which is basically the spanish version of what you just read) you can find it here:

If you run the code with the following command:

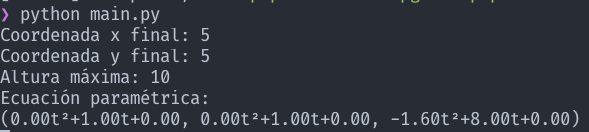
Running the command: `python main.py` (after installing dependencies)

The output will be something like these options:

Running program angle #1

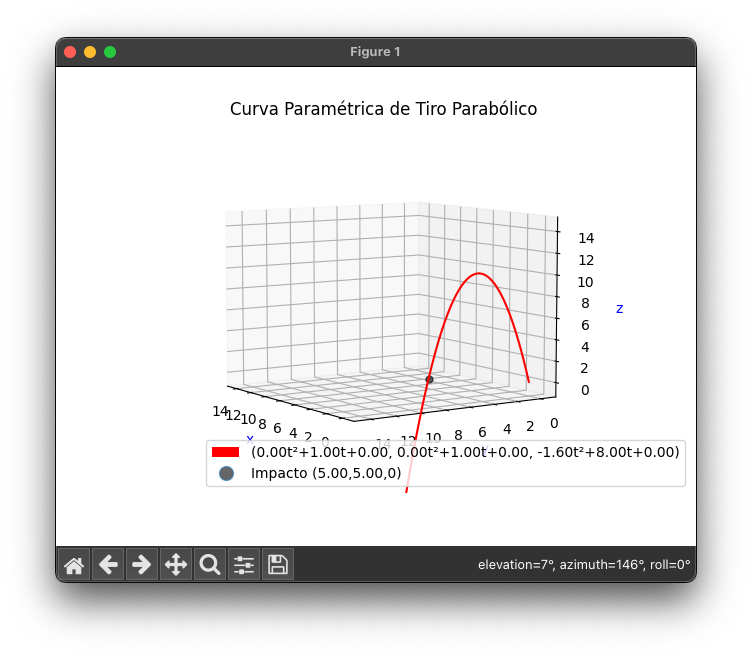
Running program angle #2

Thank you for reading! I hope you can find some inspiration here to make some cool visualizations for your classes.